Rats have up to 70 whiskers on their faces, varying hugely in size, and shape.
Rat whiskers can vary hugely.
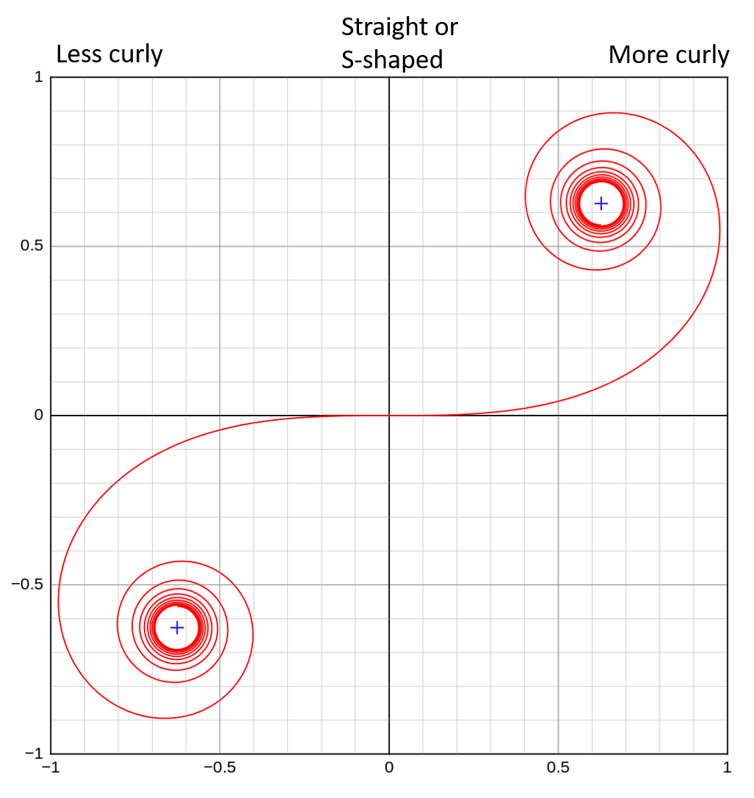
We found thatrat whiskers can be accurately described by a simple mathematical equation known as the Euler spiral.

Its an example of how special spiral patterns are found throughout the natural world.
And spotting them can help us not only understand nature better, but also improve our own engineering.
Some are s-shaped, some get more curly towards the tip and some get less curly towards the tip.

It’s free, every week, in your inbox.
Euler spiral of rat whiskers
Courtesy of Dr Eugene Starostin, London South Bank University/University College London.
Most natural structures dont display all of these three shapes.
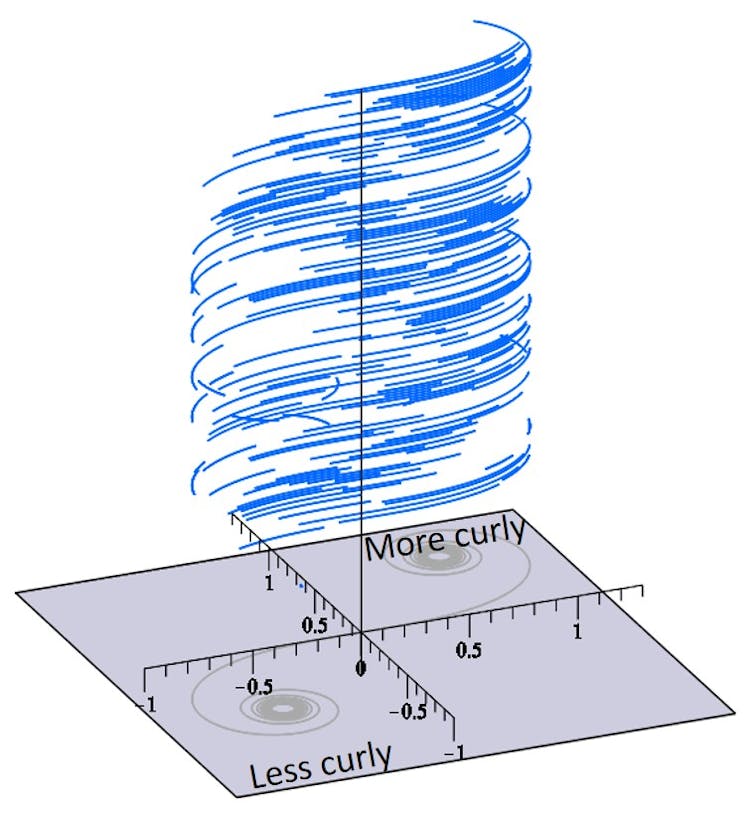
But there are many spirals in nature that get more curved along their length.
Tightening spirals in nature.
Euler discovered Bernoullis equation and started to characterize aspects of the curve that it describes in 1744.

It has even been used for finding the best route a racing car should takethrough a corner.
Rat essentials
But how can it help us to study the rat?
Describing the shapes and patterns of natural structures using simple mathematical equation can help us to understand their function.
Whiskers are actually made up of dead hair cells but they sit within a specialized sensitive follicle.
This information is what the rat uses to perceive objects and judge their shape, size and texture.
Image courtesy of Dr Maria Panagiotidi, University of Salford.
Nature isfull of mathematical patterns.
In this way, maths can give us a special insight into how biological structures and systems work.
Also tagged with

