While a model that generates predictions that arent too far off from the true value has low variance.
Since its already going beyond the real patterns of the data, the model isoverfittingthe data.
This is where regularization comes in!
In practice, regularization tunes the values of the coefficients.
Thats why regularization techniques are also calledshrinkagetechniques.
Regularization techniques are also calledshrinkage techniques, because they shrink the value of the coefficients.
Some coefficients can be shrunk to zero.
Even though its commonly used for linear models, regularization can also be applied tonon-linear models.
Wouldnt it interesting if you could predict how long your dog will nap tomorrow?
Altogether they affect your dogs energy levels and, consequently, how much they will nap during the day.
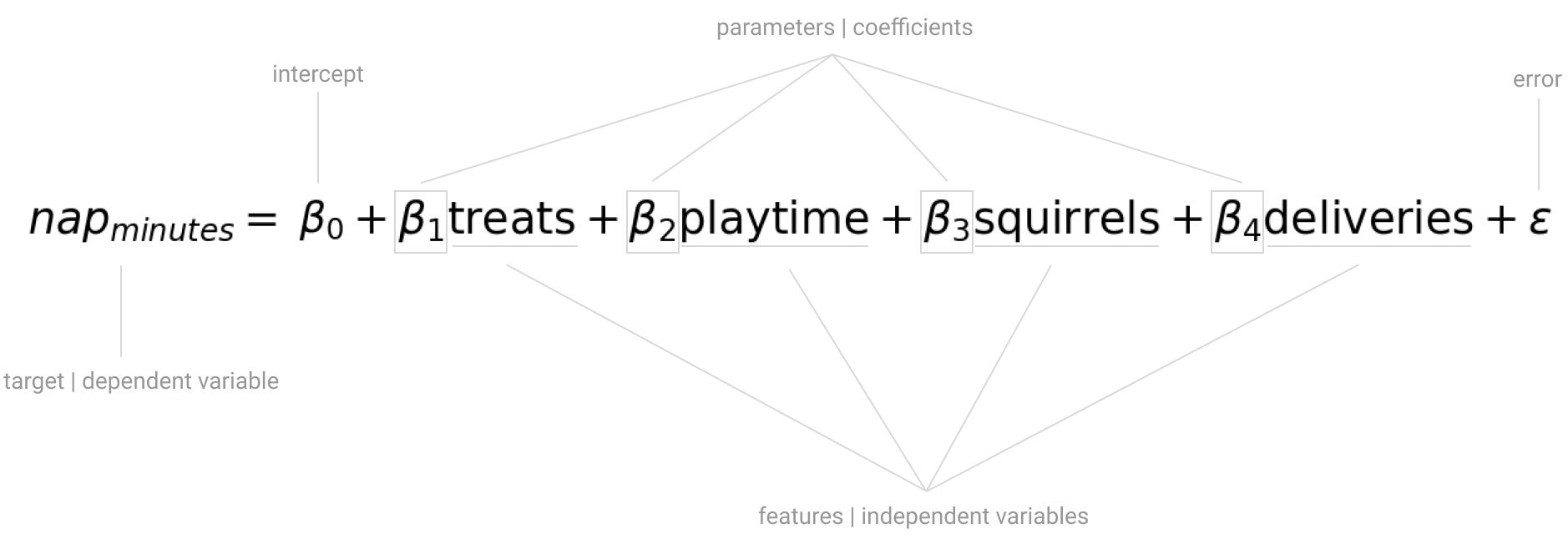
Since you want to predict your dogs nap duration, you start thinking about it as amultivariate linear model.
[Read:How do you build a pet-friendly gadget?
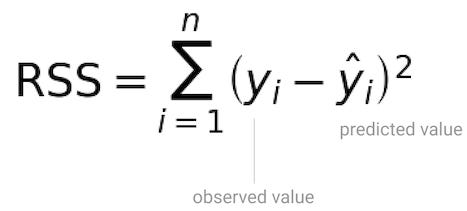
The remaining betas are the unknowncoefficientswhich, along with the intercept, are the missing pieces of the model.
Additionally, you think theres a linear relationship between the features and the target.
For how long will your dog nap tomorrow?

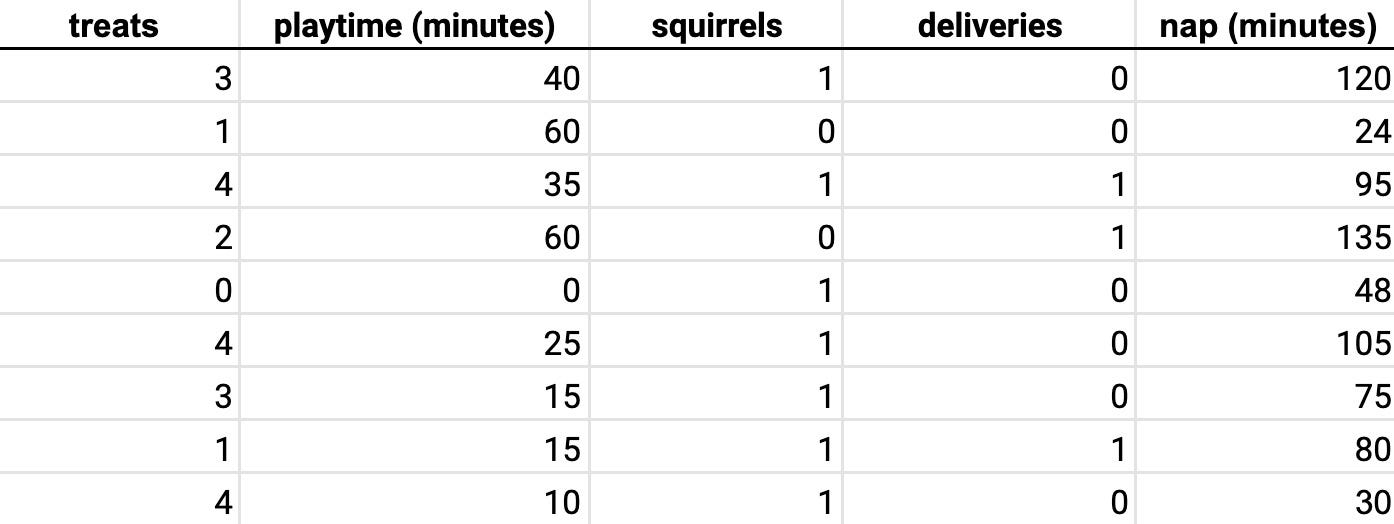
With the general idea of the model in your mind, you collected data for a few days.
Now you have real observations of the features and the target of your model.
But there are still a few critical pieces missing, the coefficient values and the intercept.

One of the most popular methods to find the coefficients of a linear model isOrdinary Least Squares.
With the residual sum of squares, not all residuals are treated equally.
In python, you could useScikitLearnto fit a linear model to the data using Ordinary Least Squares.
In this case, the test dataset sets aside 20% of the original dataset at random.
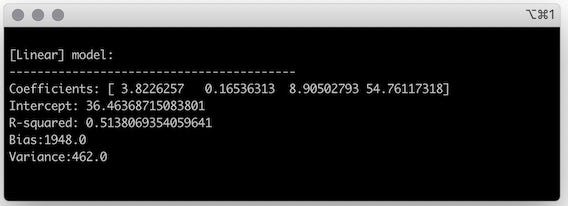
After fitting a linear model to the training set, you might check its characteristics.
The coefficients and the intercept are the last pieces you needed to define your model and make predictions.

It shows how much of the variability in the target is explained by the features[1].
Lets use regularization to reduce the variance while trying to keep bias a low as possible.
You do that by applying a penalty to the Residual Sum of Squares[1].
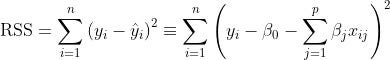
The tuning parameter controls the impact of theshrinkage penaltyin the residual sum of squares.
If all features have coefficient zero, the target will be equal to the value of the intercept.
Even though itshrinkseach model coefficient in the same proportion, Ridge Regression will never actuallyshrinkthem to zero.
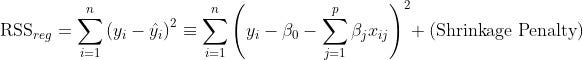
The very aspect that makes this regularization more stable, is also one of its disadvantages.
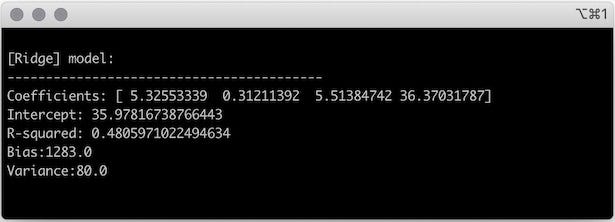
you might fit a model with Ridge Regression by running the following code.
However, the complexity and interpretability of the model remained the same.
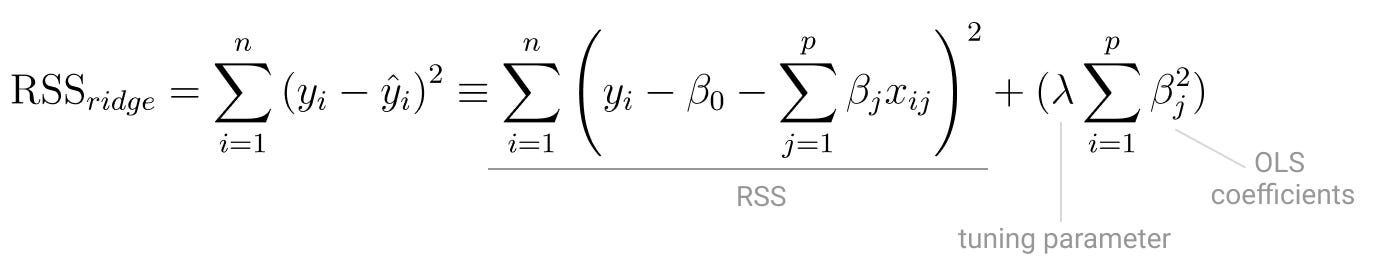
You still have four features that impact the duration of your dogs daily nap.
Lets turn to Lasso and see how it performs.
Thats why Lasso is also referred to as L1 regularization.
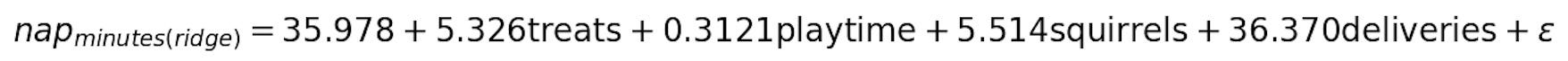
Lasso uses a technique called soft-thresholding[1].
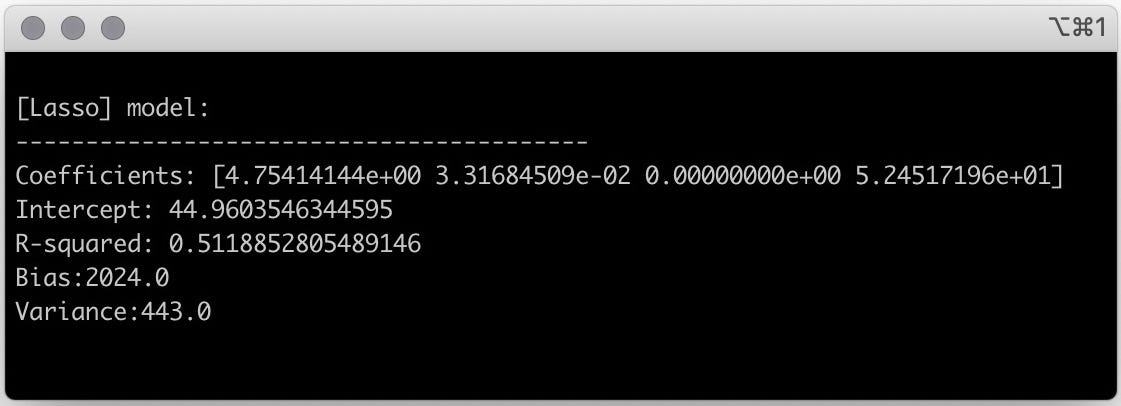
Again, with an arbitrarylambdaof 0.5, you’re free to fit lasso to the data.
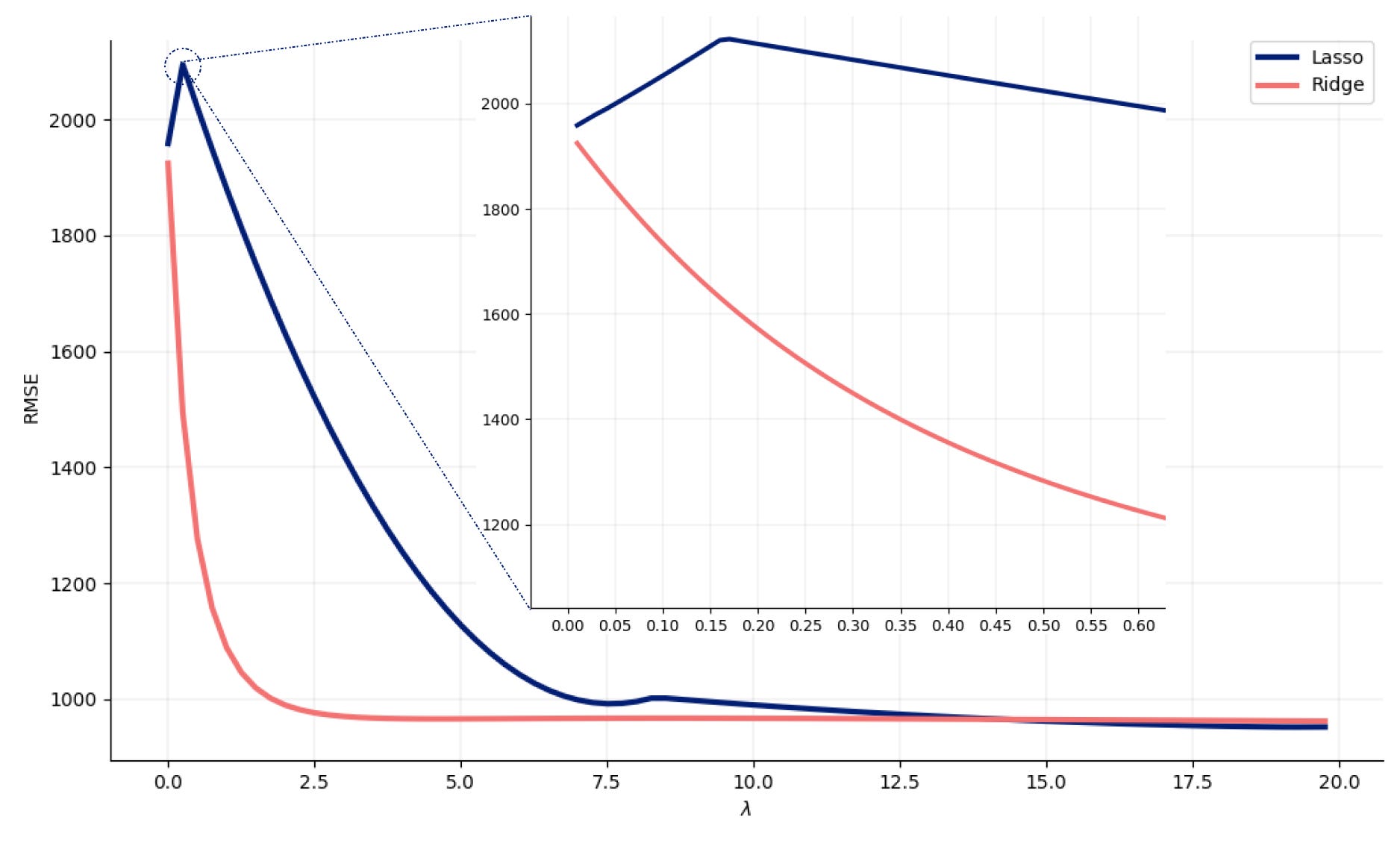
This graph reinforces the fact that Ridge regression is a much more stable technique than Lasso.
As for Lasso, theres a bit more variation.
Heres how you could create these plots in Python.
We can verify this by fitting the data again, now with more targeted values.

Using Lasso you ended reducing significantly both variance and bias.
With Ridge Regression the model maintains all features and, aslambdaincreases, overall bias and variance gets lower.
When to use Lasso vs Ridge?
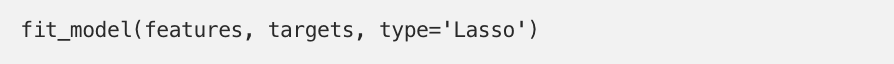
Use Lasso when …
In this case, Lasso will pick on the dominant features andshrinkthe coefficients of the other features to zero.
Use Ridge Regression when … At the end of the day, its all about trade-offs!
References
[1] Gareth James, Daniela Witten, Trevor Hastie, and Robert Tibshirani.
Regression shrinkage and selection via the lasso.
Soc B., 58, 267288
This article was originally published byCarolina BentoonTowards Data Science.
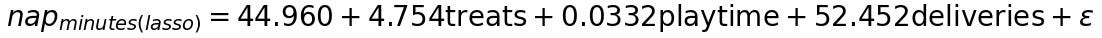
you might read the piecehere.
Also tagged with