Insights from mathematical modelling are vital to ensuring that authorities can prevent as many deaths as possible.
The S-I-R model
40% off TNW Conference!
People who have not yet had the disease are labelled susceptibles.
Everyone is assumed to be born susceptible and capable of being infected.
Those who have contracted the disease and are capable of passing it to susceptibles are the infectives.
The third group are euphemistically referred to as the removed class.
These removed individuals no longer contribute to the spread of the disease.
This model illustrates the importance of social isolation for those infected.
The outbreak cannot sustain its own spread.
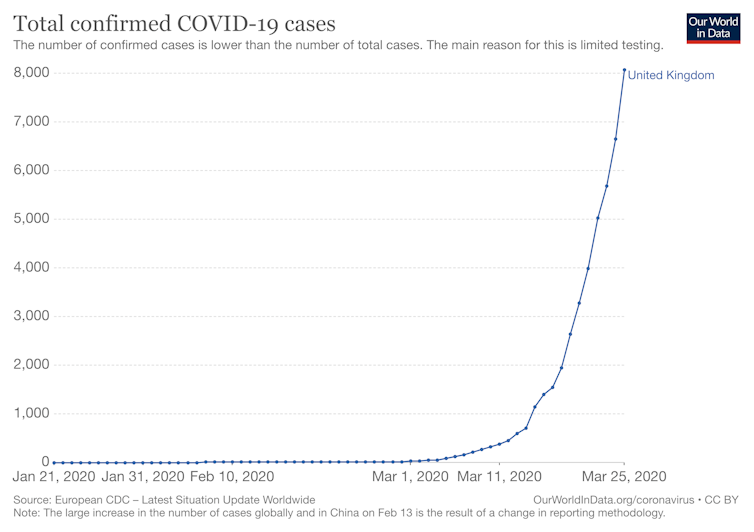
If R0 is larger than one then the outbreak will grow exponentially.
This exponential growth is characteristic of the initial phase of the infection.
Ten steps further on, the toll would rise to over one million.

Outbreaks eventually peak and then decline due to the decreasing frequency of contacts between infectives and susceptibles.
Even when there are no infectives left and the outbreak is officially over, some susceptibles will remain.
Increasing the first two of these factors increases R0, while increasing the recovery rate reduces it.
Then theres theeffectivereproduction number.
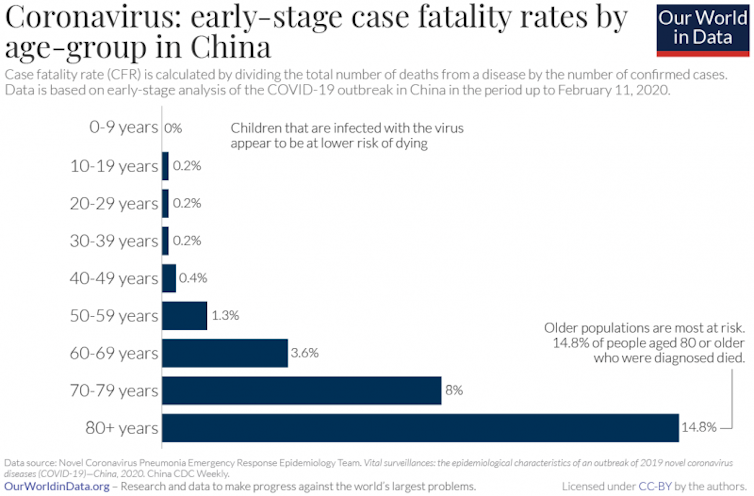
The proportion of infected people who ultimately die from a disease is known as the case fatality rate.
Early estimates indicate that the case fatality rate of COVID-19 isbetween 0.25% and 3.5%.
Controlling an outbreak
One of the most effective options for reducing disease spread is vaccination.
Quarantine and isolation can efficiently reduce the transmission rate and, consequently, the effective reproduction number.
Isolating infective patients reduces the rate of spread while quarantining healthy individuals reduces the effective susceptible population.
Food delivery workers await the orders of customers in self-isolation.
The basic reproduction number, R0, holds the key to how large that proportion is.
The higher the basic reproduction number, the higher the immune proportion of the population needs to be.
Given the case fatality rate of COVID-19, this would entail the deaths of many thousands of people.
Unsurprisingly, the UK governmentbacktracked on their proposed policy.
As is typical of some sexually transmitted diseases, gonorrhoea has no removed population at all.
Once recovered from gonorrhoea, patients can be infected again.
Since no one dies from the symptoms of gonorrhoea, no one is ever removed from the population.
Could the novel virus circulate indefinitely in the population?
During this time, people can harbour the virus and infect others without showing symptoms themselves.
That means we need to add another class of people to the model.
This changes the S-I-R model into an S-C-I-R model.
The state-of-the-art models that are currently being used to inform government policy are even more complicated.